C Program to Find Transpose of Matrix

Here is the C program to find transpose of a matrix. The transpose of a m x n matrix A, is another n x m matrix A^T by turning all the rows of a given matrix into columns and all the columns into rows.

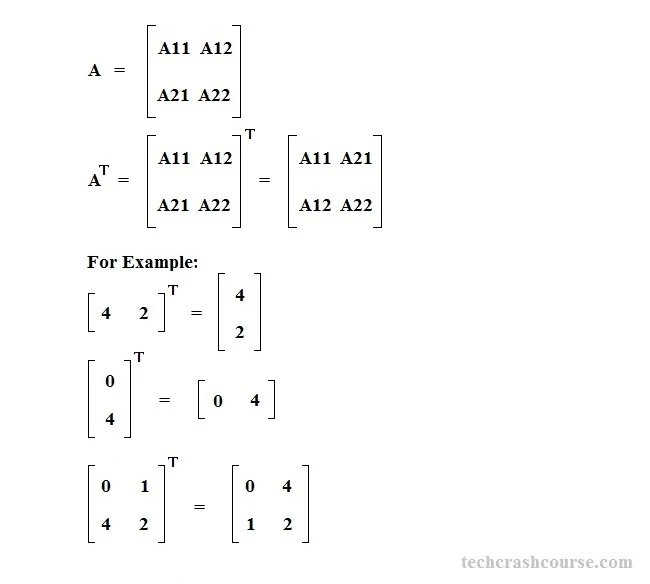
The transpose of matrix A is written A^T. The i^throw, j^th column element of A is the j^th row, i^th column element of A^T. The transpose of a matrix A can be obtained by reflecting the elements along its main diagonal. If we repeat the process of transpose on a transposed matrix A^T, it returns A with elements in their original position.

Points to Remember

The transpose of matrix A is written A^T.

The i^th row, j^th column element of A is the j^th row, i^th column element of A^T.

If A is an m × n matrix then A^T is an n × m matrix.

Algorithm to find transpose of a matrix
Let A be the input matrix of size M x N and T be the transpose matrix of A(T = A^T).

To find transpose of a matrix, we have to interchange the row and column index of every element. For example, an element of matrix A at position [i][j] will become an element of transpose matrix T at position[j][i](T[j][i] = A[i][j])

Traverse matrix A row wise(first all elements of a row from left to right, then jump to next row) using two loops(check line number 23 and 24 of below program).

For any element A[i][j], copy it's value to T[j][i](swap row and column indexes).

C program to find transpose of a matrix

#include <stdio.h>

int main(){
    int rows, cols, rowCounter, colCounter;
    int inputMatrix[50][50], transposeMatrix[50][50];
    
    printf("Enter Rows and Columns of Matrix\n");
    scanf("%d %d", &rows, &cols);
    
    printf("Enter Matrix of size %dX%d\n", rows, cols);
    
    for(rowCounter = 0; rowCounter < rows; rowCounter++){
        for(colCounter = 0; colCounter < cols; colCounter++){
            scanf("%d", &inputMatrix[rowCounter][colCounter]);
        }
    }
    
    /* transpose[i][j] = inputMatrix[j][i] */
    for(rowCounter = 0; rowCounter < rows; rowCounter++){
        for(colCounter = 0; colCounter < cols; colCounter++){
            transposeMatrix[colCounter][rowCounter] = inputMatrix[rowCounter][colCounter];
        }
    }
    
    printf("Transpose Matrix\n");
    /*Transpose Matrix of MXN  =  NXM Matrix */
    for(rowCounter = 0; rowCounter < cols; rowCounter++){
        for(colCounter = 0; colCounter < rows; colCounter++){
            printf("%d ", transposeMatrix[rowCounter][colCounter]);
        }
        printf("\n");
    }
    return 0;
}

Output

Enter Rows and Columns of Matrix
2 3
Enter Matrix of size 2X3
1 2 3
4 5 6
Transpose Matrix
1 4
2 5
3 6

Enter Rows and Columns of Matrix
3 3
Enter Matrix of size 3X3
0 1 2
3 4 5
6 7 8
Transpose Matrix
0 3 6
1 4 7
2 5 8

Properties of Transpose Matrices
Let A be the input matrix of size M x N.

The transpose of a transpose matrix is the original matrix
(A^T)^T = A

The transpose of two added matrices is the same as the addition of the two transpose matrices
(A + B)^T = A^T + B^T

When a scalar element is multiplied to a matrix, the order of transposition is irrelevant
(sA)^T = a(A)^T

The transpose of a product of matrices equal the product of their transposes in reverse order
(AB)^T = B^TA^T