The Interpreter Design Pattern is used to model a grammar of a language using a set of classes along with an interpreter that uses the representation to interpret sentences in the language. The definitions of a language grammar is represented as hierarchical representation of Expression classes, where each expression class is cable of interpreting and evaluating itself.
Let's take an example of an algebraic expression 2 + 3. To model this expression we need ConstantExpression that represents the constant operands(2 and 3) and then AndExpression that takes two ConstantExpression expressions operands and performs addition operation. All Expression classes must implement a common interface 'Expression'.
Above expression can Modelled as :
AndExpression(ConstantExpression(2), ConstantExpression(3))
Similarly, (2 + 6) + (1 + 9) can be modelled as:
AndExpression(AndExpression(ConstantExpression(2), ConstantExpression(6)), AndExpression(ConstantExpression(1), ConstantExpression(9)))
Structure of the Interpreter Design Pattern
The Interpreter Design Pattern comprises the subsequent elements:
- Abstract Expression : This interface outlines an interpret() function that concrete interpretations must incorporate. It serves as a representation of the abstract syntax tree nodes.
- Terminal Expression : Concrete interpretations that implement the Abstract Interpretation interface for terminal symbols in the grammar. They signify the endpoints of the abstract syntax tree.
- Non-terminal Expression :Concrete interpretations that implement the Abstract Interpretation interface for non-terminal symbols in the grammar. They represent nodes with one or more child interpretations.
- Context : The contextual environment stores information that holds global significance for the interpreter. It might include variables, constants, or other contextual details needed during interpretation.
- Client : The user interface takes charge of constructing the abstract syntax tree using terminal and non-terminal interpretations. Additionally, it provides the context in which the interpretation is to take place.
Advantages of Using an Interpretive Design Technique
An interpretive design technique provides numerous benefits that enhance its utility in language interpretation:
- Componentized Structure and Scalability : This technique encourages a modular design, enabling the implementation of each expression as an independent class. This modular approach simplifies the addition of new expressions and the extension of language grammar.
- Distinctive Separation of Responsibilities : The technique mandates a clear division of responsibilities between the interpreter and language expressions, resulting in a more understandable, maintainable, and extensible system.
- Facilitated Grammar Adjustments : Implementing changes to the language grammar becomes more straightforward with this technique. New expressions can be seamlessly added, and existing ones can be modified without disrupting the overall structure of the interpreter.
- Reusable Expression Components : Components handling expressions can be repurposed across different interpreters as long as they adhere to a common interface. This encourages code sharing and minimizes redundancy.
- Adaptive Interpretation : The technique supports dynamic interpretation, allowing expressions to be interpreted at runtime based on user input or other dynamic factors. This adaptability is beneficial in situations where the language undergoes dynamic evolution.
- Flexible Integration with Design Approaches : This technique can be harmoniously integrated with other design approaches, such as the Composite pattern for managing intricate expressions or the Flyweight pattern for optimizing memory usage. This integration enhances the overall design.
- Cross-Platform Suitability : Interpreters constructed using this technique can be easily transferred across different platforms and environments. The interpretation logic remains consistent, enabling the same interpreter to operate in various contexts.
When we should use Interpreter Pattern
- It is not suitable for building a whole large interpreter for a language. It can be used when the grammar of the language is simple.
- When we want to model a simple a recursive grammar.
- When simple implementation is high priority then than efficiency.
Implementation of Interpreter Design Pattern
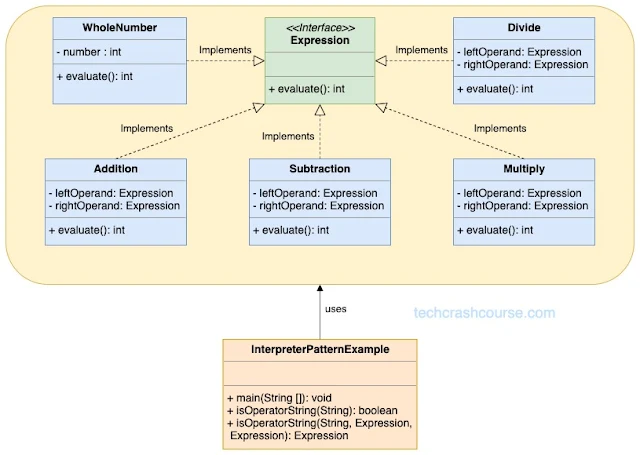
The Expression interface requires all expression classes to have common 'evaluate' method which ensure all expressions can be handled equally.
Expression.javapublic interface Expression {
public int evaluate();
}
The WholeNumber class implements the Expression interface and it represents a number operand. Inside evaluate method, it just returns the numerical value. In the arithmetic expression tree, it is known as TerminalExpressions and represents the leaf node.
WholeNumber.javapublic class WholeNumber implements Expression {
private int number;
public WholeNumber(int number) {
this.number = number;
}
public WholeNumber(String str) {
this.number = Integer.parseInt(str);
}
@Override
public int evaluate() {
return number;
}
}
Now we will create concrete implementation of Expression interface to represent Addition, Subtraction, Multiply and Division binary operations. It contains two Expressions as operands and represents the internal nodes of expression tree also known as NonTerminalExpressions.
Addition.javapublic class Addition implements Expression {
private Expression leftOperand;
private Expression rightOperand;
public Addition(Expression leftOp, Expression rightOp){
this.leftOperand = leftOp;
this.rightOperand = rightOp;
}
@Override
public int evaluate(){
return leftOperand.evaluate() + rightOperand.evaluate();
}
}
Subtraction.java
public class Subtraction implements Expression {
private Expression leftOperand;
private Expression rightOperand;
public Subtraction(Expression leftOp, Expression rightOp){
this.leftOperand = leftOp;
this.rightOperand = rightOp;
}
@Override
public int evaluate(){
return leftOperand.evaluate() - rightOperand.evaluate();
}
}
Multiply.java
public class Multiply implements Expression {
private Expression leftOperand;
private Expression rightOperand;
public Multiply(Expression leftOp, Expression rightOp){
this.leftOperand = leftOp;
this.rightOperand = rightOp;
}
@Override
public int evaluate(){
return leftOperand.evaluate() * rightOperand.evaluate();
}
}
Divide.java
public class Divide implements Expression {
private Expression numerator;
private Expression denominator;
public Divide(Expression numerator, Expression denominator){
this.numerator = numerator;
this.denominator = denominator;
}
@Override
public int evaluate(){
try {
return numerator.evaluate() / denominator.evaluate();
} catch (ArithmeticException e) {
System.out.println("Division by Zero Exception");
throw e;
}
}
}
InterpreterPatternExample is the arithmetic expression parser that takes a postfix expression and evaluate it using above expression classes. In postfix representation of an expression the operator comes after the operand. Example (1 2 +) is the postfix representation of (1 + 2)
InterpreterPatternExample.javaimport java.util.Stack;
public class InterpreterPatternExample {
public static void main(String args[]) {
Stack stack = new Stack();
String postFix = "5 3 * 2 + 1 - 4 /"; // (5 * 3 + 2 - 1)/4
String[] tokenList = postFix.split(" ");
for (String s : tokenList) {
if (isOperatorString(s)) {
Expression rightOp = (Expression)stack.pop();
Expression leftOp = (Expression)stack.pop();
Expression operator = getOperatorHandler(s, leftOp,
rightOp);
int result = operator.evaluate();
stack.push(new WholeNumber(result));
} else {
Expression num = new WholeNumber(s);
stack.push(num);
}
}
System.out.println(((Expression)stack.pop()).evaluate());
}
public static boolean isOperatorString(String str) {
if (str.equals("+") || str.equals("-") || str.equals("*") || str.equals("/"))
return true;
else
return false;
}
public static Expression getOperatorHandler(String str, Expression left,
Expression right) {
switch (str) {
case "+":
return new Addition(left, right);
case "-":
return new Subtraction(left, right);
case "*":
return new Multiply(left, right);
case "/":
return new Divide(left, right);
default:
return null;
}
}
}
Output
4
Important points about Interpreter pattern
- Interpreter can be used to implement a simple language grammar.
- This pattern comes under behavioral design pattern.
Effective Approaches for Interpreter Design Guidelines
To ensure a resilient and maintainable implementation of the Interpreter Design Guidelines, adhere to these effective approaches:
Related Topics
- Precise Grammar Definition: Clearly articulate the grammar for the interpreted language, encompassing terminal and non-terminal symbols along with their associations. A well-defined grammar is essential for crafting interpreters that are both expressive and accurate.
- Distinguish Terminal and Non-terminal Expressions: Maintain a distinct separation between terminal expressions (leaves) and non-terminal expressions (nodes) in your implementation. This enhances code clarity and simplifies grammar extension.
- Apply Composite Pattern for Expressions: In cases where the grammar involves intricate expressions with nested structures, contemplate adopting the Composite Pattern to represent expressions as composites of simpler counterparts. This streamlines the creation and interpretation of intricate expressions.
- Modularized Design: Structure your interpreter with a modular design, assigning each expression class to handle a specific language construct. This approach fosters code organization and ease of maintenance.
- Employ Context for State Information: Leverage the context to store and manage state information relevant to interpretation. The context proves valuable for storing variable values, constants, or other data essential during the interpretation process.
- Implement Robust Error Handling: Devise error-handling mechanisms to address invalid or unexpected input. This is pivotal for providing meaningful feedback when interpreting expressions that deviate from the prescribed grammar.
- Explore Results Caching: Depending on the nature of your interpreter, contemplate the incorporation of caching mechanisms to retain and reuse previously computed results. This can significantly enhance performance, particularly for expressions with recurring subexpressions.
- Adhere to Uniform Naming Conventions: Adopt uniform and meaningful naming conventions for your expression classes. This practice facilitates developers in comprehending the purpose of each class and its role within the interpreter.
| Mediator Design Pattern |
| Bridge Design Pattern |
| Prototype Design Pattern |
| Builder Design Pattern |
| Factory Design Pattern |
| List of Design Patterns |