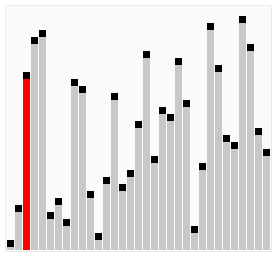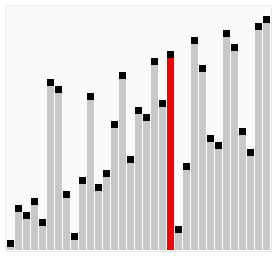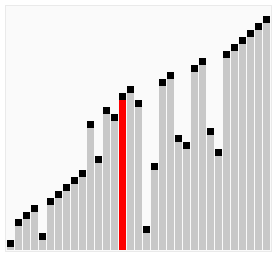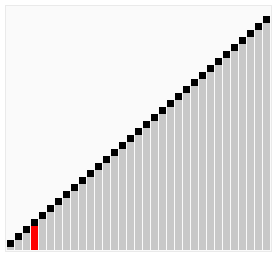
Bubble Sort is one of the simplest sorting algorithms in computer science. It is easy to understand and implement, making it a good starting point for beginners to learn about sorting algorithms. Bubble Sort is also known as Sinking Sort because it sinks smaller elements to the bottom of the array during each pass. Here is a graphical representation of bubble sort being performed on a 33 element array.
How Bubble Sort Works
Bubble Sort algorithm compares adjacent elements in an array and swaps them if they are not in the correct order. In each pass, the largest element bubbles up to the end of the array. The algorithm repeats this process until the array is sorted.
Step by Step Algorithm of Bubble Sort
The steps involved in Bubble Sort algorithm are as follows:- Start from the first element of the array and compare it with the next element.
- If the next element is smaller, swap them.
- Move to the next element and repeat the comparison and swapping process until the end of the array.
- Once the first pass is complete, start the second pass from the first element again and repeat the same comparison and swapping process.
- Continue this process until all elements are sorted.
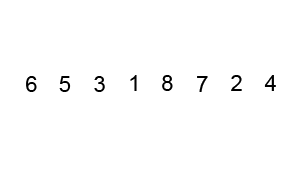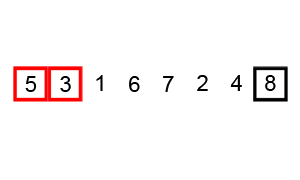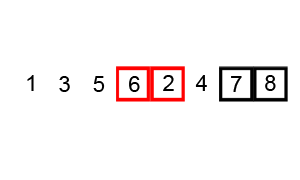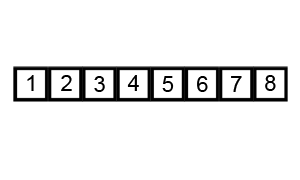
Bubble Sort Implementation in C
#include <stdio.h>
void bubble_sort(int array[], int n) {
int i, j, temp;
for(i = 0; i < n-1; i++) {
for(j = 0; j < n-i-1; j++) {
if(array[j] > array[j+1]) {
temp = array[j];
array[j] = array[j+1];
array[j+1] = temp;
}
}
}
}
int main() {
int array[] = {64, 34, 25, 12, 22, 11, 90};
int n = sizeof(array)/sizeof(array[0]);
int i;
printf("Unsorted array: ");
for(i = 0; i < n; i++) {
printf("%d ", array[i]);
}
bubble_sort(array, n);
printf("\nSorted array: ");
for(i = 0; i < n; i++) {
printf("%d ", array[i]);
}
return 0;
}
Output
Unsorted array: 64 34 25 12 22 11 90 Sorted array: 11 12 22 25 34 64 90
Time and Space Complexity of Bubble Sort
The time and space complexity of Bubble Sort algorithm depends on the number of elements in the array.
- Best Case: The best case scenario is when the array is already sorted. In this case, Bubble Sort algorithm will only perform one pass to check if the array is sorted. Therefore, the time complexity in the best case is O(n).
- Average Case: In the average case scenario, Bubble Sort algorithm will perform n-1 passes, where n is the number of elements in the array. In each pass, the largest element bubbles up to the end of the array. Therefore, the time complexity in the average case is O(n^2).
- Worst Case: The worst case scenario is when the array is sorted in reverse order. In this case, Bubble Sort algorithm will perform n*(n-1)/2 comparisons and swaps. Therefore, the time complexity in the worst case is O(n^2).
The space complexity of Bubble Sort algorithm is O(1) because it uses only a constant amount of extra memory to perform the sorting.
Advantages and Disadvantages of Bubble Sort
The main advantage of Bubble Sort is its simplicity and ease of implementation. It is also stable, which means that it preserves the order of equal elements in the sorted array.
However, Bubble Sort algorithm has several disadvantages. It is very inefficient for large arrays or datasets, especially in the worst case scenario. It takes a lot of time to sort the elements, which can be impractical for real-world applications. In addition, Bubble Sort algorithm is not adaptive, which means that it cannot take advantage of pre-sorted or partially sorted arrays to reduce the number of comparisons and swaps.
In conclusion, Bubble Sort algorithm is a simple and straightforward sorting algorithm that is easy to understand and implement. However, it is not very efficient for large datasets and has several drawbacks compared to other sorting algorithms. Therefore, it is mostly used for educational purposes and small datasets with few elements.
