
Graph Data Structure
A graph is a non-linear data structure that consists of nodes (also called vertices) and edges that connect them. Each edge connects two nodes and can be directed or undirected. Graphs can be used to represent complex networks, such as social networks, transportation networks, and computer networks.
Understanding how to represent and manipulate graphs is a valuable skill for any programmer.

Graph Terminology
- Node (Vertex): A point in the graph that represents an entity.
- Edge: A line connecting two nodes that represents a relationship between them.
- Directed Graph: A graph where the edges have a direction (i.e., they are one-way).
- Undirected Graph: A graph where the edges do not have a direction (i.e., they are bidirectional).
- Weighted Graph: A graph where the edges have a weight or cost associated with them.
- Degree of a Node: The number of edges incident to a node.
- Path: A sequence of edges that connects a sequence of vertices.
- Cycle: A path that starts and ends at the same node.
Applications of Graph Data Structure
- Social networks: Graphs can be used to represent social networks and analyze relationships between people.
- Transportation networks: Graphs can be used to model transportation networks and find the shortest path between two locations.
- Computer networks: Graphs can be used to represent computer networks and find the most efficient routing paths.
- Image processing: Graphs can be used to represent images and analyze the relationships between pixels.
Advantage and Disadvantage of Graph Data Structure
Advantages of Graph
- Graphs are powerful for modeling and representing relationships between entities, making them suitable for a wide range of applications.
- Graphs provide a flexible and dynamic structure that can adapt to various scenarios, allowing for the representation of complex systems.
- Graphs are used in diverse applications, including social networks, routing algorithms, recommendation systems, and more.
Disadvantages of Graph
- Depending on the representation chosen, graphs can have higher storage overhead, especially for sparse graphs.
- Some graph algorithms, such as finding the shortest path in a weighted graph, can have computational complexity that grows with the size of the graph.
- Cyclic dependencies in graphs can lead to challenges in certain scenarios, such as deadlock situations in resource allocation systems.
Graph Representation
There are two common ways to represent a graph: adjacency matrix and adjacency list.
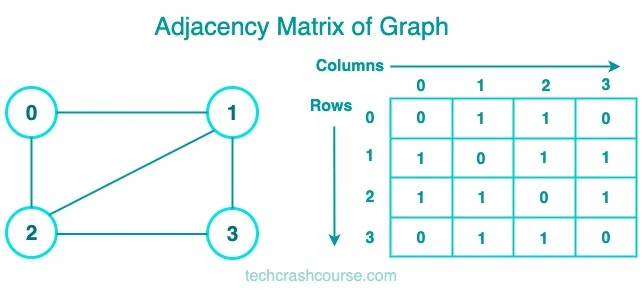
Adjacency Matrix
An adjacency matrix is a 2D array of size n x n, where n is the number of nodes in the graph. The value at matrix[i][j] represents the edge weight between nodes i and j. If there is no edge between two nodes, the value is usually set to infinity or 0.
Advantages of Adjacency Matrix
- Checking whether two nodes are connected takes O(1) time.
- The matrix can be easily used for matrix operations, such as finding the shortest path.
Disadvantages of Adjacency Matrix
- The matrix can be memory-intensive, especially for sparse graphs.
- Adding or removing nodes or edges can be time-consuming.
Implementation of a graph data structure as adjacency matrix in C
We will define a struct to represent the graph and use a two-dimensional array to store the adjacency matrix.
#include <stdio.h>
#include <stdlib.h>
#define MAX_VERTICES 100
// Define a struct to represent the graph
typedef struct {
// Number of vertices in the graph
int numVertices;
// Adjacency matrix to store edges
int adjMatrix[MAX_VERTICES][MAX_VERTICES];
} Graph;
// Function to create a new graph with the specified number of vertices
Graph* createGraph(int numVertices) {
// Allocate memory for the graph struct
Graph* graph = (Graph*) malloc(sizeof(Graph));
// Set the number of vertices
graph->numVertices = numVertices;
int i, j;
for (i = 0; i < numVertices; i++) {
for (j = 0; j < numVertices; j++) {
// Initialize all edges to 0 (no edge)
graph->adjMatrix[i][j] = 0;
}
}
return graph;
}
// Function to add an edge to the graph
void addEdge(Graph* graph, int src, int dest) {
// Set the edge weight to 1 (we're assuming an unweighted graph)
// Since this is an undirected graph, we set both directions
graph->adjMatrix[src][dest] = 1;
graph->adjMatrix[dest][src] = 1;
}
// Function to print the adjacency matrix for the graph
void printGraph(Graph* graph) {
printf("Adjacency Matrix:\n");
int i, j;
for (i = 0; i < graph->numVertices; i++) {
for (j = 0; j < graph->numVertices; j++) {
printf("%d ", graph->adjMatrix[i][j]);
}
printf("\n");
}
}
int main() {
// Create a graph with 5 vertices
Graph* graph = createGraph(5);
// Add edges between vertices
addEdge(graph, 0, 1);
addEdge(graph, 0, 2);
addEdge(graph, 1, 2);
addEdge(graph, 2, 3);
addEdge(graph, 3, 4);
printGraph(graph); // Print the adjacency matrix
return 0;
}
Output
Adjacency Matrix: 0 1 1 0 0 1 0 1 0 0 1 1 0 1 0 0 0 1 0 1 0 0 0 1 0
In this implementation, we've defined a struct to represent the graph and used a two-dimensional array to store the adjacency matrix. We've also defined functions to create a new graph, add edges to the graph, and print the adjacency matrix. In the main function, we've created a graph with 5 vertices and added edges between some of the vertices. Finally, we've printed the adjacency matrix for the graph.
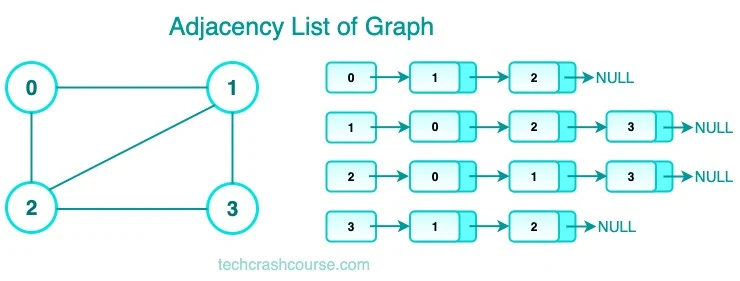
Adjacency List
An adjacency list is an array of linked lists or vectors, where each list represents the edges connected to a particular node. Each edge is represented by a pair (node, weight).
Advantages of Adjacency List
- The adjacency list can be more memory-efficient than the adjacency matrix, especially for sparse graphs.
- Adding or removing nodes or edges can be done in O(1) time.
Disadvantages of Adjacency List
- Checking whether two nodes are connected takes O(n) time.
- The list may not be suitable for matrix operations.
Implementation of a graph data structure as adjacency lists in C
#include <stdio.h>
#include <stdlib.h>
#define MAX_NODES 100
// Edge structure
typedef struct Edge {
int dest;
int weight;
struct Edge* next;
} Edge;
// Graph structure
typedef struct Graph {
int num_nodes;
Edge* adj_list[MAX_NODES];
} Graph;
// Function to create a new edge
Edge* create_edge(int dest, int weight) {
Edge* new_edge = (Edge*) malloc(sizeof(Edge));
new_edge->dest = dest;
new_edge->weight = weight;
new_edge->next = NULL;
return new_edge;
}
// Function to create a new graph
Graph* create_graph(int num_nodes) {
Graph* new_graph = (Graph*) malloc(sizeof(Graph));
new_graph->num_nodes = num_nodes;
int i;
for (i = 0; i < num_nodes; i++) {
new_graph->adj_list[i] = NULL;
}
return new_graph;
}
// Function to add an edge to the graph
void add_edge(Graph* graph, int src, int dest, int weight) {
Edge* new_edge = create_edge(dest, weight);
new_edge->next = graph->adj_list[src];
graph->adj_list[src] = new_edge;
}
// Function to print the graph
void print_graph(Graph* graph) {
int i;
for (i = 0; i < graph->num_nodes; i++) {
Edge* current_edge = graph->adj_list[i];
printf("Node %d: ", i);
while (current_edge != NULL) {
printf("(%d, %d) ", current_edge->dest, current_edge->weight);
current_edge = current_edge->next;
}
printf("\n");
}
}
int main() {
int num_nodes = 5;
Graph* graph = create_graph(num_nodes);
// Add edges to the graph
add_edge(graph, 0, 1, 2);
add_edge(graph, 0, 3, 1);
add_edge(graph, 1, 2, 3);
add_edge(graph, 2, 3, 2);
add_edge(graph, 3, 4, 4);
// Print the graph
print_graph(graph);
return 0;
}
Output
Output : Node 0: (3, 1) (1, 2) Node 1: (2, 3) Node 2: (3, 2) Node 3: (4, 4) Node 4:
Time Complexities Of Graph Operations
- Check if an element is present in the graph: O(V), where V is the number of vertices in the graph. This is because we need to traverse the adjacency list of each vertex to check if the element is present.
- Graph Traversal: O(V + E), where V is the number of vertices and E is the number of edges in the graph. This is because we need to visit each vertex and edge in the graph at most once during traversal.
- Add elements (vertex, edges) to graph: O(1) for adding a vertex, and O(1) or O(E) for adding an edge, depending on the representation of the graph. If the graph is represented using an adjacency matrix, adding an edge takes O(1) time, whereas if it is represented using an adjacency list, adding an edge takes O(E) time.
- Finding the path from one vertex to another: O(V + E), where V is the number of vertices and E is the number of edges in the graph. This is because in the worst case, we need to visit each vertex and edge in the graph during the search for the path. If we use algorithms like Dijkstra's algorithm or A* algorithm for finding the shortest path, the time complexity can be improved to O((V + E) log V) or O(E log V) respectively.
Best Practices of Graph Data Structure
- Choose the Right Representation : Select a graph representation that aligns with the specific requirements of your application. Common representations include adjacency matrix and adjacency list, each with its advantages and limitations.
- Handle Graph Traversal with Care : When traversing a graph, especially in large graphs, be mindful of efficiency. Choose the appropriate traversal algorithm based on the characteristics of your graph and the specific task at hand.
- Consider Edge Weights and Directions : If your application involves weighted or directed relationships, ensure that your graph representation and algorithms account for these properties. Incorrect handling of weights or directions can lead to incorrect results.
Conclusion
Graphs are versatile and powerful data structures that play a crucial role in modeling and solving complex problems. Understanding the fundamental concepts, types, and operations on graphs is essential for utilizing them effectively in different applications. By following best practices and considering the advantages and limitations associated with graph data structures, developers can design efficient and robust solutions. Whether optimizing routes in a transportation network or analyzing relationships in a social network, graphs remain a fundamental tool in the realm of data structures.
